
ISSN: 3005-8198 (online) / 3005-818X (print)
Volume 2, Issue 3 (July – September 2024), pp: 9-17
![]()
Experimental and Analytical Evaluation to Strengthened R.C Beams Using Ferrocement Under Torsion
Roula Taha 1,a*, Muneeb AL Allaf 1,b, Ihssan Tarsha 1, c
1 Department of Structural Engineering, Faculty of Civil Engineering, AL Baath University, Homs, Syria.
E-mail:
roula.84@hotmail.com a,*, almuneeb999@gmail.com b, ealtrshi@albaath-univ.edu.sy c,
Received: 06 May 2024 | Revised: 28 June 2024 | Accepted: 06 July 2024 | Published: 09 September 2024
The safety of structures around the globe represents a significant and pressing concern, underscoring the urgent need for the development and implementation of effective rehabilitation methods to ensure their continued functionality. Ferrocement has emerged as a durable method for the restoration of reinforced concrete (RC) structures, demonstrating resilience and versatility in addressing structural damage. A substantial body of research has been conducted to examine the mechanical properties of ferrocement, with a particular focus on its efficacy in reinforcing beams against a range of forces. In light of the limited understanding of the factors affecting the torsional strength of ferrocement-wrapped beams, it is imperative to conduct experimental investigations. The objective of this study is to evaluate and compare the torsional strength, angle of twist and crack development of different wrapping types using both analytical analysis and experimental data. The findings indicate that three-sided wrapping is an effective method for enhancing torsional behaviour, as evidenced by both experimental and analytical results. Furthermore, the utilization of styrene-butadiene rubber (SBR) as a connecting material has been demonstrated to be an effective method for maintaining cohesion across reinforced beams.
Keywords: Ferrocement, Torsion, Strengthening, Wire Mesh, Styrene-Butadiene Rubber (SBR), Beams, Crack, Twist, Torsional Strength.
It would be inaccurate to suggest that the deterioration of numerous structures worldwide is an exaggeration. The lifespan of a structure and its capacity to bear loads are influenced by a number of factors, including overloading, environmental impacts and exposure to external deteriorating agents such as fire (Takla and Tarsha, 2020). It is therefore essential to repair and rehabilitate these structures in order to ensure their continued functionality in an efficient manner (Rajguru & Patkar, 2022). Furthermore, sustainability practices in construction techniques have become the guiding vision and future direction for development (Raydan et al., 2022).
The efficacy and resilience of ferrocement as a flexible material and reinforcement method for the restoration of damaged reinforced concrete (RC) structures has been demonstrated on numerous occasions over time (Alzabidi et al., 2023). A substantial body of experimental research has been conducted to assess the physical and mechanical characteristics of ferrocement, including its efficacy in reinforcing beams against bending, axial, and shear forces. Given the circulatory nature of torsion and the fact that the shear stress caused by torsion is concentrated near the periphery of the beam (Rahal, 2013, 2021) the application of ferrocement as a wrapping material would be an effective method of protecting distressed structures against torsion. This is achieved by upgrading the beams’ load-bearing capacities and ductility (Behera et al., 2014).
Given the paucity of research examining the factors influencing the torsional strength of ferrocement-wrapped beams, it is imperative to undertake experimental investigations on RCC beams. This will provide substantial insight into their torsional characteristics.
The process of experimentally strengthening R.C. beams is often both expensive and time-consuming, particularly when examining their behaviour under torsion. Once the model has been validated using experimental data, it can be employed to enhance analytical models and accurately predict the complex nonlinear behaviour of reinforced concrete beams (Tejaswini, 2015).
The nonlinear characteristics of ferrocement are a consequence of the intrinsic properties of the material and the complex bond formed between the wire mesh and the concrete. Cement mortar has several inherent weaknesses, including low tensile strength, significant drying shrinkage, and limited chemical resistance (Wardeh et al., 2017). Despite the growing use of styrene butadiene rubber (SBR) emulsions in mortar (Barluenga & Hernández-Olivares, 2004; Taha, 2024), the majority of studies still utilise it as a slurry (cement-SBR-water) (Alzabidi et al., 2023).
A substantial body of literature supports the use of ferrocement as an effective retrofitting technique. There is a paucity of studies that provide quantitative data on the torsional strength of beams, both experimentally and analytically. This is particularly the case with regard to beams wrapped on three and two sides.
Over the past 25 years, a multitude of analytical techniques have been employed to examine ferrocement-wrapped beams (Kumarasamy et al., 2017). The earlier experimental and analytical estimation of the torsional strength of “U”-wrapped RC beams, as conducted by Behera et al. (2014), was limited to plain beams. Behera and Dhal (2018) proposed that the torque-twist response of ferrocement-wrapped beams can be characterized by three distinct stages: the elastic stage, the cracked stage, and the ultimate stage. A study by Rajguru and Patkar (2022) assessed the torsional strength of U-wrapped reinforced concrete beams using both experimental and analytical methods. The findings indicated that the addition of further layers resulted in only a marginal enhancement in torsional strength at any given level of torsion.
The interconnection between ferrocement and the R.C beam has been identified by numerous researchers as a crucial factor. In their study, Taha (2024) employed an experimental approach to estimate the torsional strength of ferrocement-wrapped beams, with a particular focus on the bond types between the ferrocement and the reinforced concrete beams utilising shear connections and SBR. The findings indicated that the utilization of shear connections resulted in an improvement in torsional behaviour by 22% with a 15 cm spacing and by 5% with a 25 cm spacing, in comparison to those employing SBR.
Nonlinear characteristics are exhibited by ferrocement as a result of a number of factors, including cracking, inelastic material response, stiffening and softening phenomena, the complex bond between wire mesh and concrete, and other factors (Kumarasamy et al., 2017). Nevertheless, in order to achieve precise results in finite element analysis, it is essential to undertake a comprehensive modelling of material behaviour, taking into account the inherent nonlinearity.
The analysis of ferrocement-wrapped beams was conducted using a computational model derived from the Timoshenko beam finite element formulation. However, numerous researchers have presented an analysis of flanged ferrocement beams using ANSYS software. In these studies, an eight-node solid isoperimetric element was employed to investigate the composite action between ferrocement laminates and wire mesh (Aboul-Anen et al., 2009).
ABAQUS is a versatile software program that employs the finite element method for the construction of geometry and the modelling of a variety of components. Each geometry is associated with a specific set of components, which are defined in accordance with the relevant material models. Furthermore, ABAQUS is equipped with the capability to delineate the interactions between components. In nonlinear analysis, ABAQUS is capable of autonomously selecting load increments and convergence tolerances, continuously adapting them throughout the analysis to ensure the efficient attainment of accurate solutions (Tejaswini, 2015).
In light of the aforementioned considerations, ABAQUS has been selected as the modelling and analysis software for the beams that have been reinforced by ferrocement from three and two sides, respectively, in this study.
The objective of this study is to investigate the torsional resistance capacity of the six specimens of beams. The beams were cast, strengthened by ferrocement on three and two sides using SBR as a connection material, and tested under pure torsion. The experimental results were ultimately compared with those of a finite element analysis (FEA) conducted using ABAQUS for the model geometry. Nevertheless, this comparison enabled us to confirm the accuracy of the analytical model for wrapped beams with ferrocement under torsion.
Six beams, each with a cross-sectional dimension of 125 mm × 250 mm and an overall span of 1700 mm, were subjected to casting and subsequent testing.
All beams were reinforced with two 12 mm bars for tensile forces and two 12 mm bars for compressive forces, each with a yield stress of 445 MPa. Furthermore, stirrups composed of mild steel with a diameter of 8 mm and spaced at 100 mm intervals were integrated into the beams, as illustrated in Figure 1. The stirrups exhibited a yield stress of 408 MPa.
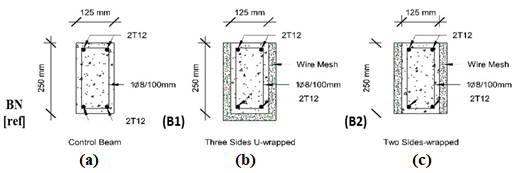
Figure 1. The Cross Sections of Control Beam and Strengthened Beams.
The reinforced concrete beams were constructed utilizing cement, sand, and coarse aggregates. A sieve analysis was conducted on the gravel in order to verify the requisite mechanical properties of the material. The results demonstrated that the tested specimens exhibited an optimal gradation. Additionally, an equivalent test for sand was conducted, yielding an average sand equivalent test value of 0.95 for the washed sand, as illustrated in Figure 2a, 2b.
The components were meticulously blended by combining Portland cement with water in a precise ratio of 0.5. To improve workability and achieve high strength with minimal water content, Flocrete SP33 was incorporated at a ratio of 1.5% to the cement weight. Subsequently, the concrete cubes exhibited a compressive strength of 25 MPa after 28 days (six cylinders were cast and tested, as illustrated in Figure 2c), with a measured tensile strength of 2.8 MPa.
Two beams were designated as reference beams, which were not subjected to any strengthening measures. The remaining beams were divided into two groups for subsequent analysis. B1 was strengthened with ferrocement on three sides (U) (Figure 1b), while B2 was strengthened on two sides (Figure 1c).

Figure 2. Testing Mechanical Properties of The Material.
The mortar mixture was formulated to ensure optimal adhesion, thereby facilitating the desired connection. The mortar mixture was prepared by combining cement, sand, and water in a 1:2.5:0.3 ratio, with the addition of SBR (polymer emulsion) at a 20% cement ratio (calculated as the mass of the solid phase of polymer emulsion divided by the mass of cement). This process has been demonstrated to be effective in achieving high adhesion between ferrocements and beams, as evidenced by numerous research studies (Siddiqi et al., 2013). A compressive test of the ferrocement mortar was conducted by casting and testing samples measuring 4×16×4 cm on site. The average value obtained was 25 MPa (Figure 2d).
Prior to the commencement of the retrofitting process, the surfaces of the beams and the bonding face of laminates were subjected to sandblasting, which served to expose the aggregates and create a roughened texture. Subsequently, any debris was meticulously removed from the surface using an air jet (Alzabidi et al., 2023).
In order to implement the ferrocement strengthening system, a square woven wire mesh was constructed using iron with a diameter of 2.5 mm and spaces between the wires measuring 20 mm. The mesh exhibited a yield strength of 568 MPa, as determined through tensile testing of a representative sample in accordance with the recommendations set forth in ACI 549.1R-93.
Subsequently, the requisite length of the mesh layer was excised and shaped to the desired configuration, accommodating variations in wrapping from three sides (Figure 3a) and from two sides (Figure 3b).
The wire mesh was positioned over spacers with a height of 10 mm, and the free ends of the mesh were secured with metal tie strips when the wrapping was from three sides. In the case of a two-sided wrapping, the opposing ends of the mesh were fastened at the top and bottom in order to provide a provisional fastening until the application of cement mortar. Subsequently, the tie strips were trimmed.

Figure 3. Beams’ Strengthening Process by Ferrocement From Two and Three Sides.
The experiments were conducted at the laboratory of the Department of Civil Engineering, AL-Baath University. Figure 4 depicts the testing apparatus utilized for the assessment of all RC beams. The beams, with a length of 1700 mm, were subjected to a twist from both ends by means of two opposing twist arms. All beams were subjected to a twist from both ends by means of two opposing twist arms. The aforementioned arms, measuring 40 cm in length, are situated at either end of the beam. The support conditions were implemented with the objective of generating a free rotation of the extremities of the beams under examination. The distance between the connecting points of the arms and the beam is 1500 mm. The I-steel beam was positioned on the twist arms with the intention of transferring the load from the mechanical screw to the arms, which subsequently subjected the beams to torsion. The displacement of the tested beams was recorded during the incremental loading process by means of five sensors (LVDT).
The ultimate torsional strength and corresponding angle of twist of each specimen were determined up to the point of total failure.
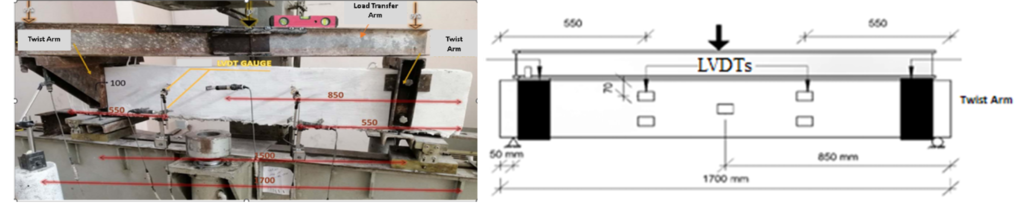
Figure 4. Torsion Test Rig and Sensors Locations.
The load was increased in incremental steps until the point of failure was reached. Thereafter, the average readings of the sensors’ gauges were logged, and the twist angles of the beams were calculated. The torsional strength of each beam was evaluated at distinct stages, namely the cracked stage (defined as the point at which the first crack appears) and the ultimate stage (corresponding to the failure point). Additionally, the accompanying angle of twist for each stage was determined.
The results of the testing of the beams are presented in Table 1 in the form of the cracking torque, the ultimate torque, the twist at cracking and the ultimate twist. This enables a comparison of the variations in strengthening achieved through ferrocement.
Table 1. Experimental Results of Reference Beams and Strengthened Beams.
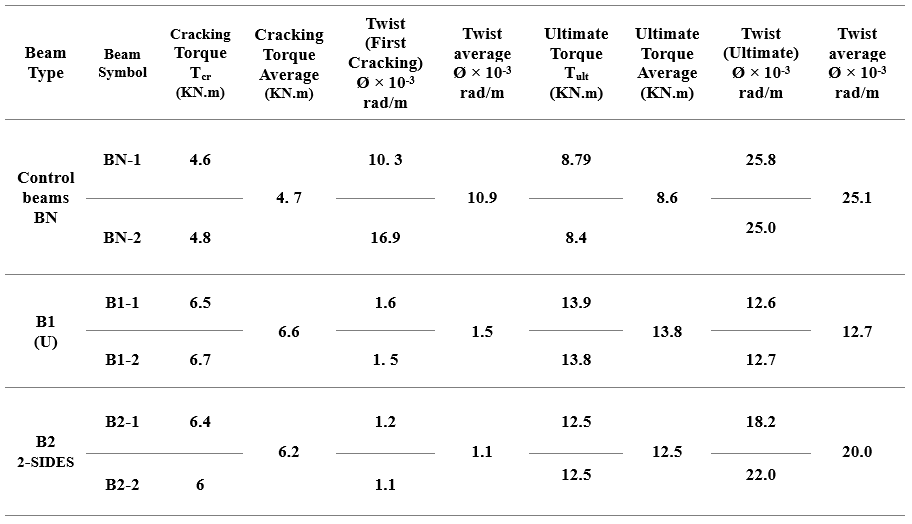
The results demonstrate a significant enhancement in the cracking strengths, ultimate strengths, and angles of twist of the strengthening beams (B1 and B2) in comparison with the control beam (BN). It is evident that there has been an improvement in both the torsional performance of the strengthening beams and their capacity to regulate cracking. The twist angle decreased from 10.9*10-3 rad/m for BN to 1.56*10-3 rad/m for B1 and 1.146*10-3 rad/m for B2 at the initial cracking point. The formation of cracks occurred at a later stage in the strengthened beams in comparison to the control beams. The initial crack appeared in B1 at a torque value of 6.6 KN.m, in B2 at 6.2 KN.m, whereas in BN, it was at 4.723 KN.m. It has been demonstrated that ferrocement, when used as a wrapping technique, exhibits the capability to withstand spiral cracks induced by torsion, thereby enhancing the control of cracking behaviour in strengthened beams subjected to torsional moment. Additionally, the ultimate torque of the strengthening beams demonstrated a notable increase, reaching 60% for the beams wrapped on three sides and approximately 43% for those strengthened on two sides, as illustrated in Figure 6.
An examination of the relationship between torque and twist in control beams, as well as those wrapped with U-wrapping and 2-sides wrapping with SBR connection (as illustrated in Figure 5), can provide valuable insights into the impact of strengthening on failure behaviour.
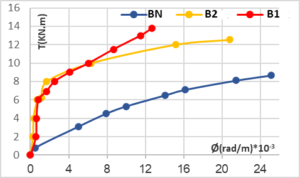
Figure 5. The Relationship Between the Torque and the Twist of Tested Beams.
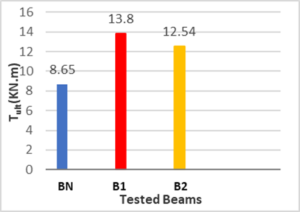
Figure 6. The Average Value of Ultimate Torque of Tested Beams.
While the control beams displayed predominantly linear characteristics in response to torsion, the behaviour of B1 and B2 exhibited two distinct stages. Both beams demonstrated linear behaviour until reaching the initial crack point, which occurred at 6.6 KN.m and 6.2 KN.m, respectively. Subsequently, B1 and B2 transitioned into the elastic-plastic stage until reaching a torque value of 10 KN.m. Beyond this point, B1 experienced a sharp increase, reaching its peak at 13.89 KN.m, where the behaviour became predominantly plastic. In contrast, B2 demonstrated a gradual increase in torque, reaching the failure point at 12.54 KN.m, where the behaviour also became predominantly plastic.
It is evident that the three-sided wrapping exhibited the highest resistance, with the failure point occurring at approximately 14 KN.m. This suggests that the addition of a single side to the existing two-sided wrapping resulted in a considerable and disproportionate increase in the ultimate torque, as illustrated in Figure 6.
Upon visual examination in conjunction with the aforementioned results, the control beam initially developed cracks around the torsion arms, which subsequently propagated in a spiral pattern. Subsequently, a significant crack emerged in the centre of the beam. Subsequently, the cracks widened rapidly until the structure failed. Following the failure, the torque value decreased rapidly until the total collapse was reached, as illustrated in Figure 7.

Figure 7. The Cracks Propagation in BN Beams
The behaviour of the ferrocement-wrapped beams was observed to differ from that of the other components, as illustrated in Figure 8. Subsequently, the number of cracks increased rapidly. The cracks gradually widened at a slow pace until the structure collapsed. At the point of failure, the number of cracks reached a maximum, and the twist values subsequently decreased. The B2 beams exhibited a more extensive range and a more rapid rate of crack propagation.

Figure 8. The Difference of the Cracks’ Width Between B1 and B2 Beams.
It was observed that the ferrocement laminates with two-sided wrapping, using SBR to connect with the beam, experienced partial sloughing off accompanied by semi-deep cracking, as depicted in Figure 9. In contrast, the three-sided wrapping maintained its connection with the RC beams, displaying only minor hairline cracking, as shown in Figure 10. The control beam displayed brittle behaviour following the formation of the initial crack, with a notable increase in the rate of crack development compared to the strengthened beams. In the post-failure state, the beams demonstrated torque stability values within the range of 12 to 14.6 KN.m.

Figure 9. The Partial Separations of the Ferrocement Laminate in B2.

Figure 10. The Ineffective Separations of the Ferrocement Laminate in B1.
The creation of a dependable analytical simulation of a reinforced concrete structure necessitates the development of an exact model of the structural elements and their constituent members, which function as a composite comprising concrete and steel (Reddy et al., 2020). In this research, three-dimensional finite element models of a control reinforced concrete beam strengthened by ferrocement from two and three sides were developed. The finite element model was constructed using a solid element of the C8D3 type, comprising eight nodes with three degrees of freedom at each node. These are translations in the nodal x, y, and z directions, as illustrated in Figure 11. The model is capable of plastic deformation, cracking in three orthogonal directions, and crushing. This element is employed as a deformable solid body for the purposes of modelling the concrete beam, the steel twist arms and the mortar.
Table 2. CDP Data and Coefficients.

The truss element of type T8D2 is employed for the modelling of steel reinforcement and wire mesh, which is characterised by two nodes with three degrees of freedom at each node, as illustrated in Figure 12. In order to model concrete, the concrete damaged plasticity (CDP) model was employed. The data and coefficients utilized in the CDP model are presented in Table 2. The discrete rigid model was employed to represent the twist arms.
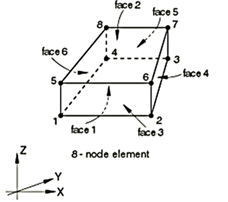
Figure 11. Solid Elements Used for Finite Element Modelling (Kumarasamy et al., 2017).
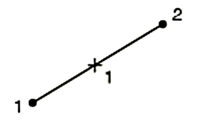
Figure 12. Truss Element Used for Finite Element Modelling (Kumarasamy et al., 2017).
In order to accurately simulate the behaviour of the tested R.C. beams, it is essential to ensure effective collaboration between the concrete and reinforcement. Accordingly, the embedded region method was employed. Similarly, a type of tie was employed to connect the twist arms and the R.C. beam. A finite element model was developed by incorporating a weld mesh element into the ferrocement mortar, as illustrated in Figure 13a.
The effects of SBR as a connection material are dependent upon the fraction coefficient, which was determined to be 0.1 (Abaqus 6.14 Documentation, n.d.; Mane & Patil, 2023).
Once the material properties had been assembled and assigned, in accordance with those utilized in the experiments, the beam was supported by two rollers at a distance of 50 mm from the edges. The load was then applied as a concentrated force at the end of each twist arm, thus creating a double torsion moment. The analytical model loading was applied in an incremental manner.
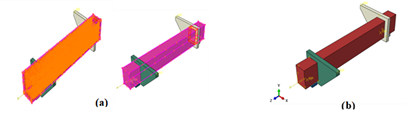
Figure 13. a: The Connection Between the Components of the Model, b: The Final Analytical Model.
The analytical results of the control beam BN, as illustrated in Figure 14 and Table 3, exhibited a comparable failure pattern to that observed in the experimental results, with minimal discrepancy. Furthermore, the formation and progression of cracks are analogous, with significant cracks developing at the same location as illustrated in Figure 15. Nevertheless, the experimental results indicate a slight increase in the ultimate torque.
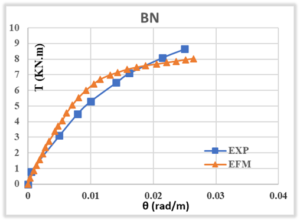
Figure 14. The Torque-Twist Behaviour of BN Beam, Experimentally and Analytically

Figure 15. The Failure Pattern of BN Beam, Experimentally and Analytically
The torque twist response of the tested beams, reinforced with ferrocement on three sides, is illustrated in Figure 17.
A comparison between the experimental test results and the analytical analysis (Figure 16) indicates that the failure mode was analogous, with cracks observed at the mid-span of the beam in both instances. Furthermore, a slight reduction in the experimental twist angle was observed, resulting in enhanced torsional stability. This suggests a strong correlation between the experimental and analytical results.

Figure 16. The Cracks Formations of B1 Beam, Experimentally and Analytically
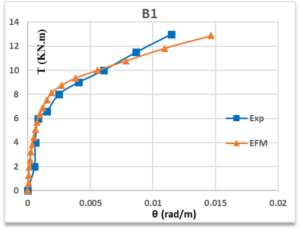
Figure 17. The Torque-Twist Behaviour of B1 Beam, Experimentally and Analytically
Figure 18 elucidates the experimental and analytical torque-twist angle relationships of B2, which was wrapped in ferrocement from two sides. This figure demonstrates that the torsional behaviour of both diagrams is comparable, although there is a slight deviation between the analytical and experimental curves. As evidenced in Table 3, there was no notable change in the cracking strength, while the experimental ultimate torque at failure points exhibited a slight increase. As illustrated in Figure 19, debonding was evident at the interface between the RC beam and the ferrocement in both instances of failure.
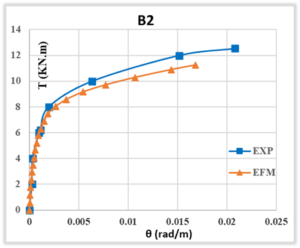
Figure 18. The Torque-Twist Behaviour of B2 Beam, Experimentally and Analytically

Figure 19. The Cracks Formations of B2 Beam, Experimentally and Analytically.
Table 3. Experimental and Analytical Results of Control Beams and Strengthened Beams
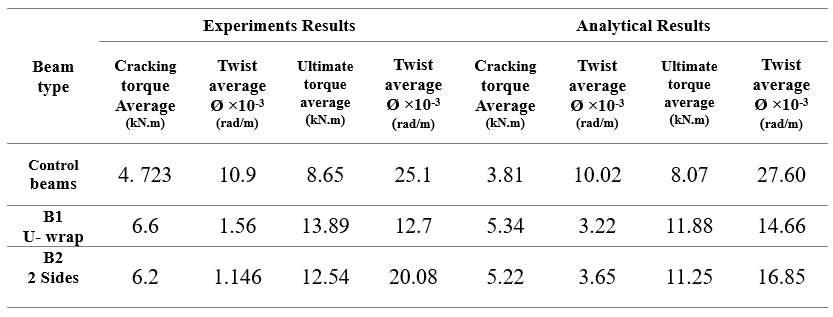
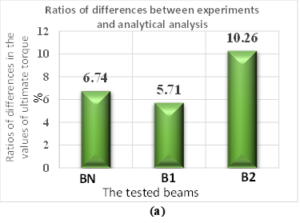
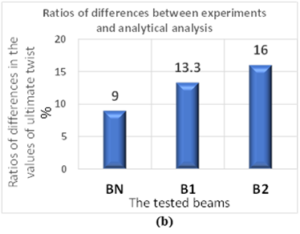
Figure 20. Ratios of Differences Value of Ultimate Torque and Twist Between Experiments and Analytical Analysis
The charts above illustrate the ratios of the discrepancies between the values of torsional moments and twist angles at failure, both in terms of experimental data and analytical modelling. The results demonstrate a consistent torsional behaviour, with values that closely align in all cases. Nevertheless, the greatest discrepancy in twist angles was observed in beams supported on two sides with ferrocement, with a variation of approximately 10%. This serves to confirm the effectiveness of the proposed FEM model in simulating the torsional behaviour observed in the experiments.
The findings of the experimental and analytical studies allow the following conclusions to be drawn:
Cite: Taha, R., Al Allaf, M., & Tarsha, I. (2024). Experimental and Analytical Evaluation to Strengthened R.C Beams Using Ferrocement Under Torsion. Steps For Civil, Constructions and Environmental Engineering, 2(3), 9–17. https://doi.org/10.61706/sccee1201121
Copyright: © 2024 by the authors. Licensee SSG, Dubai, UAE.
This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND 4.0) license (http://creativecommons.org/licenses/by-nc-nd/4.0/).






An independent academic publisher with an editorial team including many of the top researchers in the world. SSG publishes research, review, and case report articles in double-blind, peer-reviewed, open access scientific and academic journals.
Copyright © 2025 Scientific Steps International Publishing Services LLC (Dubai – United Arab Emirates)