
ISSN: 3005-8198 (online) / 3005-818X (print)
Volume 2, Issue 2 (April – June 2024), pp: 7-16
![]()
Employing Numerical Modelling to Calculate Changes in Safety Factors for The Bearing Capacity of Expansive Clay Soil Subjected to Cycles of Full Wetting and Partial Drying
Rodina Daod1,a*, Nazih Abboud1,b, Mohamad Imad Machlah1, c
1 Department of Geotechnical Engineering, Faculty of Civil Engineering, Damascus University, Syria.
E-mail: engrodina@yahoo.com a,*, dean.hiesr@damasuniv.edu.sy b, imadmach@gmail.comc
Received: 02 December 2023 | Revised: 19 January 2024 | Accepted: 25 March 2024 | Published: 26 April 2024
Soil mechanics provides a theoretical framework for understanding the behaviour of soil in relation to structures and the extent to which it is influenced by various natural and unnatural factors. A series of laboratory experiments on soil are conducted in its current condition, without consideration of potential long-term changes to its specifications and behaviour. Furthermore, the implications of these changes on the most crucial soil calculations, namely bearing capacity and safety factors, are not addressed. This prompted us to emphasise the potential risks associated with the failure to consider the changes that occur in clay soils. In this research, the findings of prior experiments on expansive soils subjected to cycles of complete wetting and partial drying were used as a basis for numerical modelling using the MATLAB program. This resulted in the derivation of mathematical equations that express the changes with the number of cycles. The Hansen relationship was employed for the calculation of the bearing capacity of the soil, as well as for the determination of the safety factors. A clear decline was observed in the bearing capacity values for the various soil types under investigation. Additionally, a notable reduction in safety factor values was identified, with some soils exhibiting a decrease exceeding 40%. This is a significant concern due to the potential for substantial material and human losses. It was thus imperative to consider the impact of wetting and drying cycles when conducting laboratory experiments to ascertain the actual safety factors in structures.
Keywords: Modelling, Safety Factors, Bearing Capacity, Wetting Drying Cycles, Expansive Soil.
The term ‘soil bearing capacity’ is of paramount importance in the field of structural soil mechanics. Any miscalculation of this parameter will inevitably result in structural damage to the edifice constructed upon it. The application of pressure in excess of the soil’s bearing capacity results in the formation of cracks in the structure built upon it, which may ultimately lead to its collapse. This, in turn, gives rise to significant financial and human losses (Yeni, 1988). It is the responsibility of the civil engineer to conduct accurate field and laboratory investigations into the soil in question, to analyse the results of said investigations, and to determine the characteristics of the soil and its components. The presence of clay minerals, for instance, has a significant impact on the geometric behaviour of the soil. (Das, 2010). This is what prompted geotechnical engineers to pursue further research into clay soils. The objective of the research was to gain insight into the behaviour of these soils in general and in the context of immersion in water in particular. Researchers began to investigate the behaviour of these soils and the changes that occur during the wetting and drying cycle. Expansive soils were the focus of research attention due to the significant deformations they exhibit. These deformations manifest as settlement, caused by the shrinkage of the soil as it dries out, or as swelling, caused by the soil’s absorption of water. This can result in the formation of cracks and, in extreme cases, structural collapse. Such phenomena manifest as swelling in pavements and deformation of floor slabs. The extent of these deformations may vary considerably, depending on the degree of swelling (Al-Muhaidib, 2002). The “Electrical double layer” phenomenon posits that the swelling of clay soil is attributable to the presence of negative charges on the surface of clay grains. These negative charges attract cations (positive ions) existing in water solutions, concentrating them and positioning them on the surface of the clay granules. In other words, negatively charged clay metals will attract positive ions. This process of sharing positive and negative ions is referred to as the “electrical double layer” phenomenon. The electrolytes present in the electrolyte layer possess the capacity to absorb water (hydrone) energy. This is arranged in a specific direction under the influence of a field of electrical forces, and the water bound on the surface forms a water membrane. The formation of the water membrane results in an increase in the distance between soil particles, leading to soil swelling (Liang et al., 2010). The theory of microstructure posits that expansive soils exhibit deformation (swelling and shrinkage) that is not solely determined by the intrinsic composition of the material, but also by the specific arrangement and spatial distribution of its components within the material’s precise structure. It is postulated that the constituents of the expansive soil material are the foundation for deformation, while the attributes of the microstructure establish the spatial configuration that gives rise to swelling and contraction. When the aforementioned fundamental conditions are satisfied, expansive soil will undergo expansion when it gains water and contraction when it loses water (Liang et al., 2010).
A substantial body of reference studies has demonstrated the adverse effects of expansive soils on engineering facilities. Furthermore, the methods employed to implement wetting and drying cycles on the soils in question, along with the resulting experimental outcomes, have been elucidated. One of the most significant references, namely that of Laura and Stephen (1986), demonstrates the outcomes of a series of laboratory experiments conducted with the objective of attaining a more profound comprehension of the resistance characteristics of highly plastic clay soils employed in the construction of dams. It was discovered that the long-term shear resistance in the field was significantly lower than that observed in laboratory experiments on compacted samples. Furthermore, the application of safety factors based on reduced laboratory resistances for dams that collapsed.
It was established that a significant reduction in safety factors occurs as a consequence of wetting and drying cycles. Nevertheless, the calculated factors of safety remain marginally above one, even when the reduced shear strength due to wetting and drying is taken into account. Consequently, further laboratory experiments are required to elucidate the impact of wetting and drying on the long-term resistance properties of highly plastic clay. While laboratory experiments to determine soil resistance to shear are reliable, they do not yet enable us to rely on them for predicting the long-term stability of dams constructed of highly plastic clay. It is evident that these cohesion values should not be relied upon for the design of highly plastic clay soils when they are subjected to repeated wetting and drying (Laura & Stephen, 1986). Furthermore, the researchers investigated the impact of wetting and drying cycles on the durability characteristics of soil. Their findings indicated that the internal friction angle and cohesion of clay soils exhibited a decline with an increase in the number of cycles to which these soils were subjected. This conclusion was corroborated by Hossain et al. (2016).
A further study demonstrated a reduction in the values of both cohesion and the angle of internal friction (Hossain et al., 2016). This was observed with cycles in accordance with the equations derived for both cohesion and angle of friction with the number of cycles, as illustrated in Figure 1.

Figure 1. Changes in Both Cohesion and The Angle of Internal Friction with Cycle Number (Hossain et. al, 2016).
Another study demonstrated that climate changes, such as repeated wetting and drying over geological time, result in the breakdown of parent rocks and the formation of soil. Concurrently, these actions can also result in the aggregation of soil particles and the formation of bonds, designated as “drought bonds,” which transfer effective stress to the soil. The effective stress can influence the shear strength behaviour of soils that are subjected to such climatic actions. The application of effective stress to soil in a laboratory setting, through repeated wetting and drying, has been observed to result in increased shear strength and a more robust response to stress and deformation. This effective stress can be attributed to the presence of chemical bonds within the soil matrix (Allam & Sridharan, 1981).
The objective of the research is to analyse the results of laboratory experiments conducted on samples of expansive soil, which were exposed to cycles of full wetting and partial drying. The aim is to identify the durability factors at each of the cycles which they were exposed to, with the objective of establishing appropriate relationships that express the changes that may occur in these factors. This will be achieved by modelling the results using a specialized program (MATLAB). Furthermore, the aim is to ascertain the impact of wetting and drying cycles on the safety factors for the bearing capacity of expansive soils.
The research presented was based on laboratory experiments conducted in the soil mechanics laboratory at the University of Damascus. The experimental data for this study were obtained from a previous paper published in the Damascus University Journal of Engineering Sciences (Abboud et al., 2023). A large number of soil samples from across the Syrian Arab Republic were tested to determine their physical properties, with the aim of identifying the type and classification of these soils based on a set of international classifications. The objective was to identify expansive soils. For soils identified as expansive, undisturbed samples were obtained and subjected to cycles of full wetting and partial drying. This entailed wetting the samples until they reached their maximum free swelling value and then drying them until they returned to their natural moisture content. Furthermore, the time required for each sample to reach its maximum swelling value and subsequently undergo partial shrinkage was determined. The results were validated through the application of the aforementioned cycles. Subsequently, shear experiments were conducted in the direct shear device for each of the ten soils following each cycle. The resulting shear specifications and observed changes were then determined.
Initial direct shear experiments were conducted on three undisturbed samples with a shear speed of 0.5 mm/min. This speed was selected based on the soil type and the shape and type of loads that will be applied at the site. It should be noted that increasing the speed can result in lower values of cohesion and angle of friction. Prior to applying cycles, the Mohr-Coulomb envelope was drawn, and the cohesion values and initial angle of internal friction were determined. Subsequently, three additional shear samples of the same soil were subjected to a single cycle of full wetting and partial drying, after which the shear specifications were determined. Subsequently, three additional shear samples from the same soil were subjected to two cycles of full wetting and partial drying, after which the shear specifications were determined. Consequently, the aforementioned cycles were repeated on new samples until equilibrium was reached, which occurred at the fifth cycle.
As a result, a minimum of 60 direct shear experiments were performed on specimens extracted from the ten approved expansive soils. The direct shear tests were conducted in accordance with the procedure outlined in ASTM D3080. In light of the findings that multiple cycles exert a discernible influence on the characteristics of expansive soils, it proved beneficial and crucial to commence processing the existing data with the objective of conducting numerical modelling and identifying mathematical equations that correlate the soil’s cohesion and angle of internal friction with the number of wetting and drying cycles applied. The MATLAB program was selected for this purpose, as it is regarded as a sophisticated programming language for digital and graphical calculations and the development of numerous applications. This system was developed with the objective of assisting engineers and other professionals engaged in scientific fields to complete tasks that require extensive digital processing in a more expeditious and precise manner.
A comprehensive geotechnical study was conducted on a substantial number of soil samples. The objective was to ascertain the possibility of deducing mathematical relationships based on statistically sound foundations. In the initial phase of the investigation, particle size analysis (sieves and hydrometer) (ASTM D422) and Atterberg limit tests (ASTM D4318) were conducted and compared with the approved classifications. This was done to ascertain whether the soil in question was expansive clay. In the second stage of the study, undisturbed samples of the expansive soil were taken and subjected to a series of experiments designed to ascertain their physical and mechanical properties. This was done prior to initiating the application of the specified cycles.
Table 1. Results Used to Classify Soils.
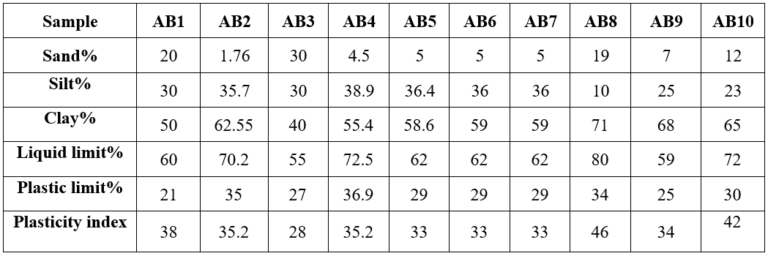
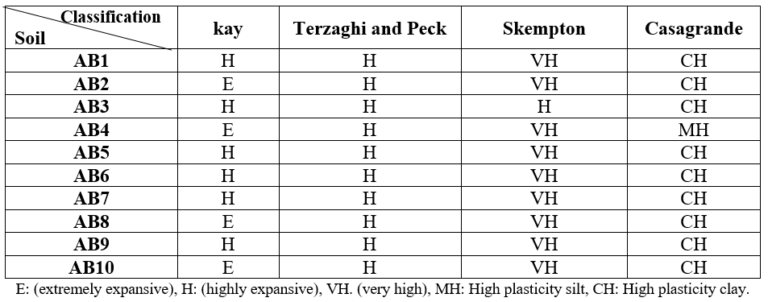
In light of the aforementioned results, and in accordance with the classification of soil in terms of swelling potential as outlined by Kay (1990) (Brigatti et al., 2006), the classification of soil in terms of swelling potential as proposed by Terzaghi and Peck (1967) (Brigatti et al.) was also considered. The classification of soil in terms of swelling potential according to Skempton (1953) (Brigatti et al., 2006) and the classification of Casagrande (1932) (Al-Homoud et al., 1995) both categorize the soils as expansive. This is demonstrated in Table 2.
Table 2. Classification of the Ten Soils Studied.
Approximately 60 direct shear experiments were conducted on undisturbed samples of soil that were described as expansive soils. The objective was to determine the changes in soil cohesion values and the angle of its internal friction as a result of exposure to repeated cycles. Prior to the application of the aforementioned cycles to the soil, a series of shear experiments were conducted. Subsequently, the test was repeated on samples that had been subjected to repeated cycles. The cycle comprised a phase of wetting that lasted for three days, followed by a phase of partial drying that continued for a period of time that varied according to the specific characteristics of the soil in question. In a previous study, we outlined the methodology for determining this period for each of the ten soil types under investigation (Abboud et al., 2023).
Table 3 illustrates the impact of wetting and drying cycles on soil cohesion (Abboud et al., 2023). Table 4 illustrates the impact of wetting and drying cycles on the angle of internal friction of soil, as demonstrated by Abboud et al. (2023).
Table 3. Changes in Cohesion Values Under the Influence of Cycles C (kN/m²).
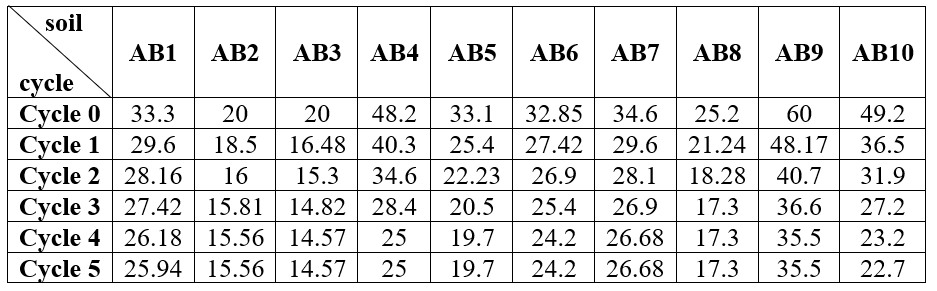

Figure 2. Changes in Cohesion Values Under the Influence of Cycles (kN/m²).
Table 4. Changes in the Angle of Internal Friction Under the Influence Cycles (ϕ°).

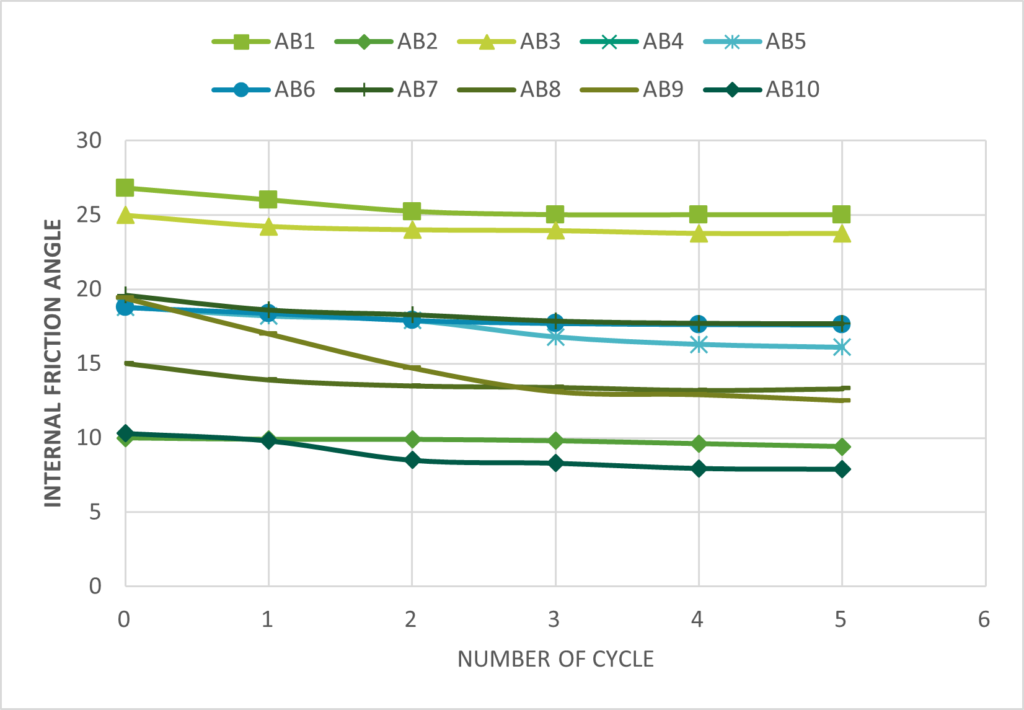
Figure 3. Changes in The Angle of Internal Friction Under the Influence of Cycles (ϕ°).
In order to achieve the research objectives of identifying mathematical equations that link the cohesion and angle of internal friction of expansive soils across a range of wetting and drying cycles, MATLAB program was employed. This entailed a series of steps, beginning with the restructuring of the data to align with the work plan and then examining the relationship between each of the nineteen inputs. The variables included in the study were as follows: water content (x1), unit weight (x2), specific gravity (x3), sand content (x4), silt content (x5), clay content (x6), liquid limit (x7), plastic limit (x8), shrinkage limit (x9), plasticity index (x10), swelling index (x11), cohesion (x12), internal friction angle (x13), shrinkage ratio (x14), void ratio (x15), dry unit weight (x16), free swelling (x17), linear shrinkage (x18), shrinkage index (x19) were correlated with the outputs (cohesion, angle of internal friction), Subsequently, an attempt was made to ascertain the form of the relationship between the variables (inputs) and the results (outputs). Finally, using MATLAB instructions, a final relationship was established between the cohesion and the angle of internal friction with the selected variables. The validity of the relationship was verified by comparing its results with the results of laboratory tests.
The results of the specific laboratory tests on the physical and mechanical properties of the studied soils are presented in Table 5, which was compiled in the form of an input matrix.
Table 5. Properties of the Studied Soils (Matrix x).
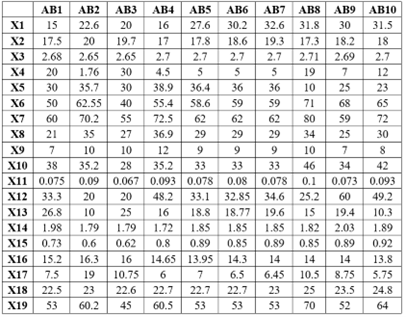
A new matrix, designated XX, was constructed as the input matrix and replicated six times for each cycle. The sequence of instructions was devised to restructure the data in a manner that would allow for each experiment to be repeated six times with identical inputs, with only the cycle number varying.
The correlation between each of the nineteen variables and the values of cohesion and the angle of internal friction is investigated using the MATLAB program.
The following series of instructions was employed to ascertain which variables exhibited the highest correlation with the cohesion values. The correlation between all 19 variables and the cohesion values was investigated. The process commences with the formation of a loop, which is repeated 19 times, corresponding to the number of variables. In each repetition, the relationship between one of the variables and the cohesion values is studied. Subsequently, the drawing window is divided into several sections, with points representing the relationship between one of the 19 variables and the values (C) drawn in each section. The correlation coefficient between the current variable and the cohesion values (C) is obtained using the (corr) instruction. Figure 4 illustrates the relationship between cohesion and the various specifications, with the number indicating the specification and the correlation coefficient displayed below. The correlation between this specification and cohesion.
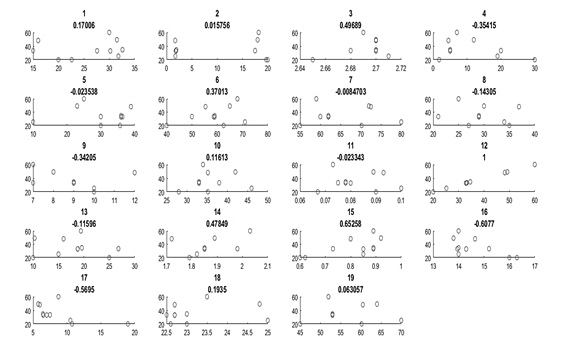
Figure 4. The Relationship of Each of The Variables with Cohesion.
The preceding series of instructions was employed to ascertain the variables most closely associated with the angle of internal friction, and the diagrams depicted in Figure 5 were generated.
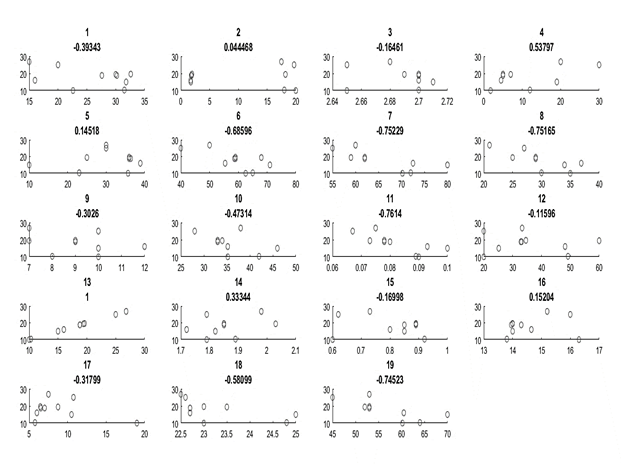
Figure 5. The Relationship of Each of The Variables with The Angle of Internal Friction.
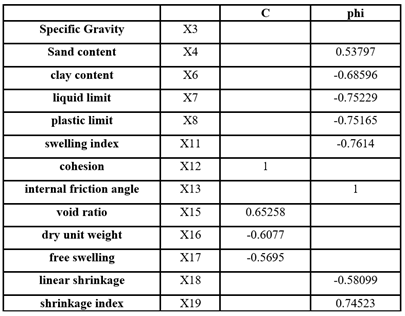
Table 6 presents a summary of the results of the correlation study. In accordance with the data presented in Table 6, the following entries were selected for the purpose of identifying the requisite equations, given that they exhibit the highest correlation coefficients.
Table 6. Results of The Study of The Correlation Between Inputs and Outputs.
A series of instructions were employed to extract the requisite data from the Excel file, and the (cftool) tool was used to plot the potential for a dependent relationship between each selected variable and both the cohesion and the angle of internal friction.
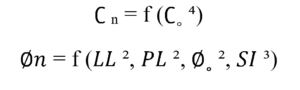
The (fitlm) instruction was employed to ascertain the mathematical relationships between cohesion and the angle of internal friction, as well as the variables selected for each of these variables. This instruction requires the input of the variables associated with the aforementioned relationships, as well as the degree to which these relationships were previously identified.
A final relationship was identified between the cohesion observed during the different cycles and the variable previously adopted, namely the initial cohesion (before the cycles) (X12), in addition to the number of wetting and drying cycles. (X20)
In accordance with the instructions provided by Excel, the variable values are stored within a separate variable in vector form. This vector is then utilized in the fitlm tool for the purposes of usability.
A drawing window is opened, and the data is transformed into a tabular format. Subsequently, the tabulated data and the requisite relationship form are transferred to the film function, which generates a relationship in accordance with the data between the specified variables and the dependent variable. This is then stored in a statistical model, designated the (predict).
MATLAB gives the results as follows:
c ~ 1 + x12 + x20 + x12^2 + x12^3 + x12^4
Estimated Coefficients:
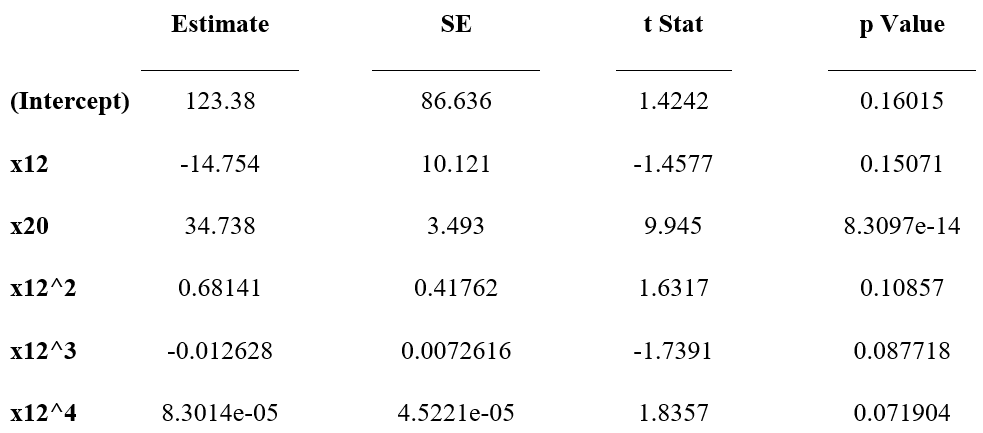
Number of observations: 60, Error degrees of freedom: 54
Root Mean Squared Error: 3.5
R-squared: 0.879, Adjusted R-Squared: 0.867
The final relationship that expresses the changes in cohesion values of expansive soils with the change in the number of cycles is as follows:
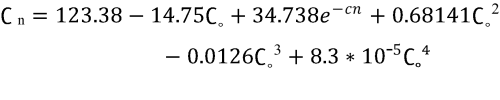
“∁ n” : cohesion over different cycles (kN/m²).
“∁˳” : initial cohesion (kN/m²).
cn : cycle number.
The veracity of the relationship was corroborated through the construction of a diagrammatic representation, wherein the laboratory cohesion values were shown to converge with the cohesion values calculated mathematically using the statistical model. This convergence was demonstrated by the bisector of the first quadrant, which was drawn and given a title on both the horizontal and vertical axes. The resulting diagrammatic representation took the following form:
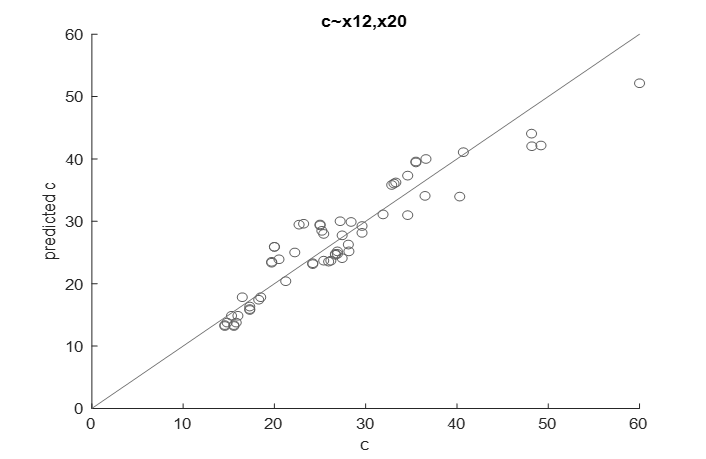
Figure 6. Convergence of Laboratory and Computational Cohesion Values.
A final relationship was identified that elucidates the alterations in the values of the angle of internal friction throughout the various cycles and the variables that were previously adopted, namely: the initial angle of internal friction (prior to the cycles) (X13), the liquid limit of the soil (X7), the plastic limit (X8), and the shrinkage index (X19). Furthermore, the wetting and drying cycle number (X20) was also considered.
A series of instructions analogous to those employed for cohesion were implemented, yielding the following outcome:
Linear regression model:
phi ~ 1 + x7 + x8 + x13 + x19 + x20 + x7^2 + x8^2 + x13^2 + x19^2 + x19^3
Estimated Coefficients:
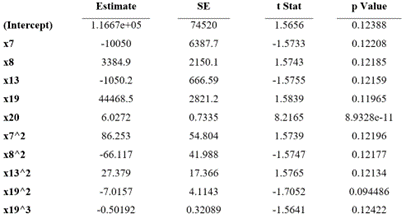
Number of observations: 60, Error degrees of freedom: 49
Root Mean Squared Error: 0.735
R-squared: 0.984, Adjusted R-Squared: 0.981
The final relationship, which expresses the changes in the values of the internal friction angle for expansive soils with the change in the number of cycles, is as follows:

∅n: the angle of internal friction during different cycles (˚)
“∅˳” :the initial angle of internal friction (˚).
LL : Liquidity limit (%)
PL,: Plastic limit (%)
cn∶ Cycle number
SI∶ shrinkage index.
In order to verify the validity of the relationship, a diagram was constructed which demonstrated the convergence of laboratory internal friction angle values towards the mathematically calculated internal friction angle values utilising the statistical model. The bisector of the first quadrant was drawn, and a title was assigned to both the horizontal and vertical axes. This resulted in Figure 7:

Figure 7. Convergence of Laboratory and Calculated Internal Friction Angle Values.
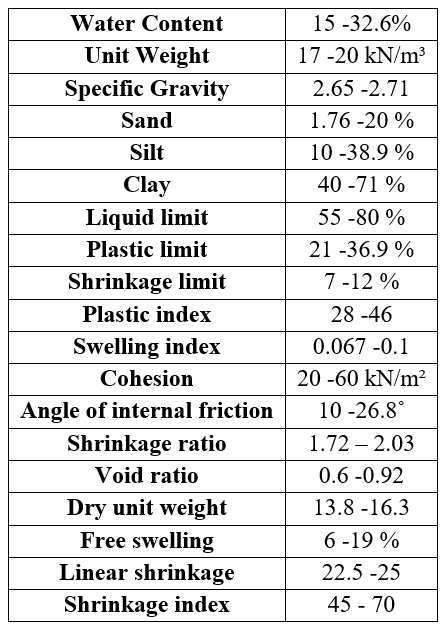
It can thus be stated that the values of cohesion and the angle of internal friction of the soil can be determined after a specific number of complete wetting-partial drying cycles for soils that meet the specified limit conditions. The following table presents the boundary conditions applicable to the soils under consideration in this study:
Table 7. Boundary Conditions for Soils.
The loads borne by the structures are conveyed to the surrounding soil through the foundations. The foundation is the component of the structure that is in direct contact with the soil and serves to transfer the loads from the structure to the soil. The selection of an appropriate foundation type is primarily dependent upon the value of the soil bearing capacity. The term “soil bearing capacity” is defined as the maximum pressure that can be applied to the soil base underlying the foundation (Yeni, 1988). A plethora of theoretical frameworks and analytical techniques exist that facilitate the calculation of soil bearing capacity. Among these is Prandtl analysis, which represents one of the earliest solutions to the problem of determining soil bearing capacity. Another is Terzaghi’s analysis, which built upon Prandtl’s work and provided insights into the bearing capacity of soil beneath surface foundations. He failed to take into account the strength of the soil located within the foundation depth D, assuming that it was solely influenced by its weight. Furthermore, he regarded the foundation as being of a rough nature. In addition to the Meyerhof, Vesic and Hansen relationships, which introduced modifications to Terzaghi’s equation regarding foundation shape and load placement, the J. Hansen relationship is recommended for calculating the bearing capacity of fine-grained soil (Yeni, 1988). This is consistent with the soil types under consideration in this study, which are clay soils.
The bearing capacity of soil according to Hansen is given by:
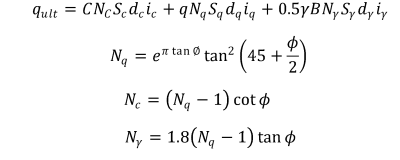
Table 8. Shape Factors.
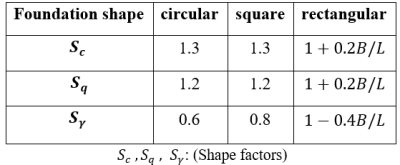
Table 9. Inclination Factors.
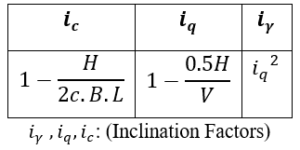
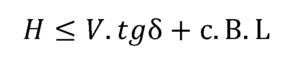
δ : The factor of friction between the foundation and the soil.
c: Cohesion between the foundation and the soil.
L: the length of the foundation parallel to H.
H, V: the horizontal and vertical forces applied to the foundation.
Table 10. Depth Factors.

In this context, the term “D” represents the foundation depth. The present study is applied to a square foundation with a width of 2 m located at a foundation depth of 2 m, subject to a central vertical load. The bearing capacity of each of the ten soils for this foundation is calculated according to the Hansen relationship, after each of the wetting and drying cycles to which it is subjected. Table 11 illustrates the alterations in safety factors for soil bearing capacity in response to the application of wetting and drying cycles.
The internal friction angles and cohesion values for diverse soil types across multiple cycles were calculated using the equations derived from the MATLAB program, which are:

Table 11. Changes in Safety Factors for The Bearing Capacity of Soils Exposed to Cycles
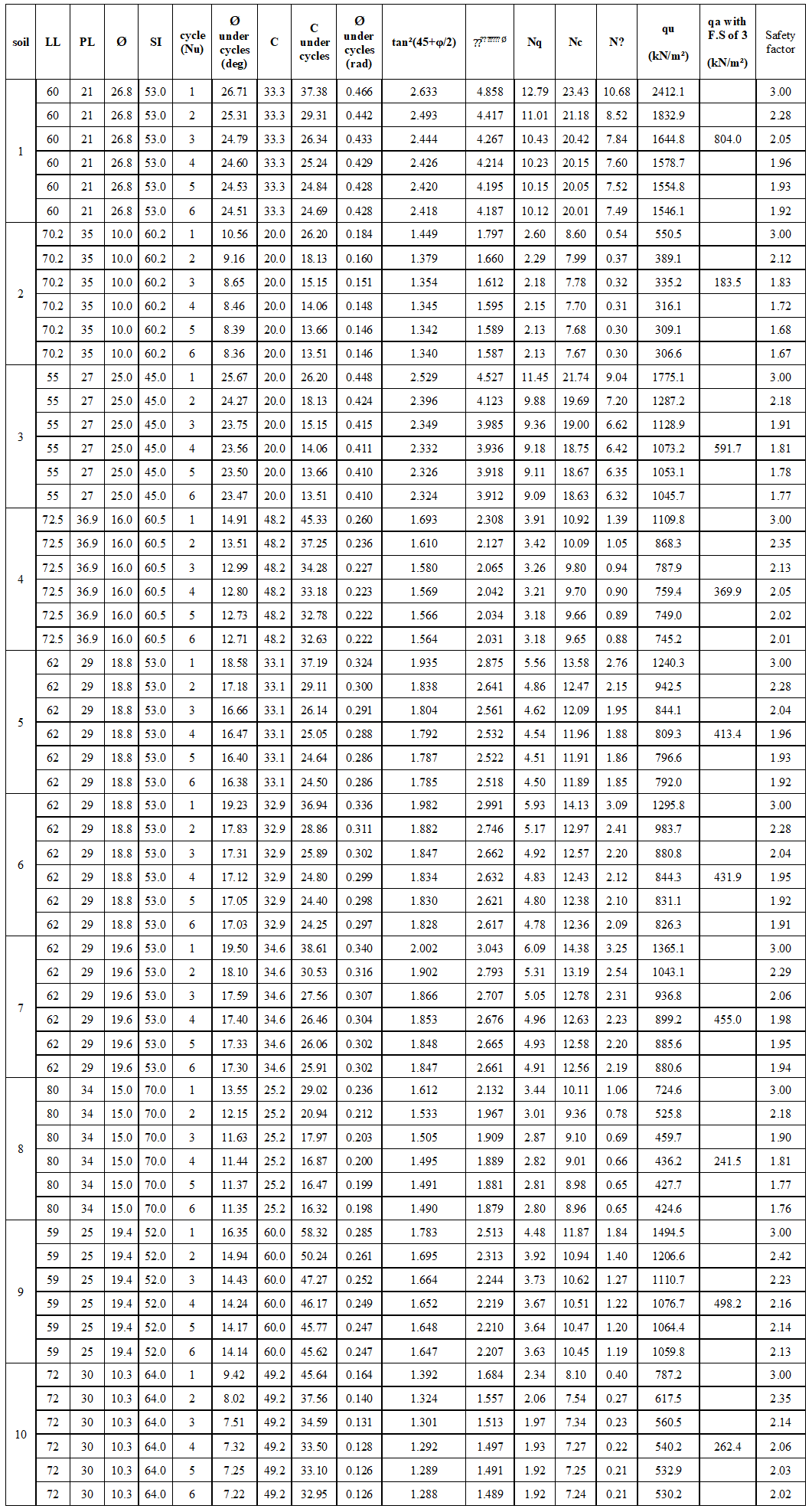
LL: Liquid Limit, PL: Plastic Limit, SI: Shrinkage Index, Ø: Angle of Internal friction, qu: ultimate bearing capacity, qa: allowable bearing capacity
Based on this data, the ultimate bearing capacity of each soil was calculated at a different number of cycles, and subsequently, the safety factor for the bearing capacity of the soil in each case was calculated. It was demonstrated that the value of the safety factor decreased markedly with the number of wetting and drying cycles to which the soil was subjected. The reduction in some soil samples reached 40%, and in some cases, the resulting safety factor values were below the acceptable threshold of 2. Figure 8 illustrates the observed decline in the safety factor.

Figure 8. Decrease in Factor of Safety with Cycles.
Table 12. Relative Change in Safety Factors for The Bearing Capacity.

The research findings demonstrate the influence of repeated soil wetting and drying cycles on the sustainability of engineering facilities. The clear change in the values of the soil’s bearing capacity and its safety factors can be observed. Furthermore, the findings of the tests indicated a reduction in the shear resistance of the soils subjected to repeated cycles of complete wetting and partial drying. It is evident that each of the shear coefficients diminishes with the increase in the number of cycles. While the decrease was not statistically significant for the internal friction angle, it was evident for the cohesion value. This illustrates the necessity of taking into account the impact of multiple cycles when establishing the mechanical properties of expansive soils. A summary of the results is presented below.
Cite: Daod, R., Abboud, N., & Machlah, M. I. (2024). Employing Numerical Modelling to Calculate Changes in Safety Factors for The Bearing Capacity of Expansive Clay Soil Subjected to Cycles of Full Wetting and Partial Drying. Steps For Civil, Constructions and Environmental Engineering, 2(2), 7–16. https://doi.org/10.61706/sccee120119
Copyright: © 2024 by the authors. Licensee SSG, Dubai, UAE.
This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND 4.0) license (http://creativecommons.org/licenses/by-nc-nd/4.0/).






An independent academic publisher with an editorial team including many of the top researchers in the world. SSG publishes research, review, and case report articles in double-blind, peer-reviewed, open access scientific and academic journals.
Copyright © 2025 Scientific Steps International Publishing Services LLC (Dubai – United Arab Emirates)